Boltzmann Generator

背景

Boltzmann 形式的分布

在广泛的条件下，统计力学所关心的微观状态 $\mathbf{x}$ 的平衡概率符合如下分布

$$\mathbf{x}\sim C \exp (-u(\mathbf{x}))\tag1$$

最为著名的例子就是 Boltzmann 分布。(1) 中的标量能量项 $u(\mathbf{x})$ 包含系统的势能、温度和可选的其他热力学量。

基于轨迹的方法: MCMC/MD

由于现阶段除去少量的模型体系外，并没有直接从 Boltzmann 分布中得到 one-shot 的样本 $\mathbf{x}$ 的方法，因此，往往使用依赖于轨迹的方法例如马尔科夫链蒙特卡洛 (MCMC) 或分子动力学 (MD) 等方法通过在每一步中逐渐微调 $\mathbf{x}$ 来对系统进行采样。由于复杂系统中亚稳态的广泛存在导致在这些状态中相互转换成为了罕见的事件 (rare events) ，这类方法往往需要非常长的时间才能得到平衡分布。这个特点使得 MCMC/MD 非常昂贵。

基于 CV 的增强抽样

为了克服 MCMC/MD 中对罕见事件的采样问题，一种常见的方法是对人为定义的的集合变量 (collective variables) 或称反应坐标 (reaction coordinates) 进行偏置 (biasing) 来加速这一过程。然而，这往往需要比较多的先验信息。对于复杂的高维系统，受限于难以获得有效的 CV 以及在其他的未偏置的方向上的能垒难以避免，这一方法很难应用。

Boltzmann Generator^[1]

Frank Noé 等人基于深度学习构建了 Boltzmann Generator (以下简称为 BG) 用以解决复杂势能面上的采样问题，其主要思路是将复杂系统的采样转化为一个简单分布的生成和从生成得到的分布向目标分布的可逆变换两个部分。通过训练一个可逆的神经网络，BG 将 $\mathbf{x}$ 映射到隐空间上的坐标表示 $\mathbf{z}$，其中不同状态的低能量配置彼此接近并且可以容易地采样 (e.g. 高斯分布)。由于 BG 是可逆的，因此，对 $\mathbf{z}$ 的采样经过一个逆向的变换，就可以得到原有微观状态 $\mathbf{x}$ 的分布，这将与原有的 Boltzmann 分布非常接近，此时，经过一个简单的重加权就可以得到原有的 Boltzmann 分布。

概览

在 BG 的框架下，对系统的采样主要需要进行如下步骤

1. 训练一个神经网络 $F_{zx}$ 使得从简单的先验分布生成 $\mathbf{z}$ 后，$F_{zx}(\mathbf{z})$ 将产生一个构想 $\mathbf{x}$ 使得 $\mathbf{x}\sim p_X(\mathbf{x})$。其中的分布 $p_X(\mathbf{x})$ 是一个接近于目标 Boltzmann 分布的分布。
2. 为了得到无偏的样本并计算在原有分布上的期望，对得到的 $p_X(\mathbf{x})$ 进行重加权，例如对于每一个样本应用如下的权重

$$w(\mathbf{x}) = e^{-u(\mathbf{x})} / p_X(\mathbf{x})$$

然后计算相关的统计量。

这一过程示于下图中

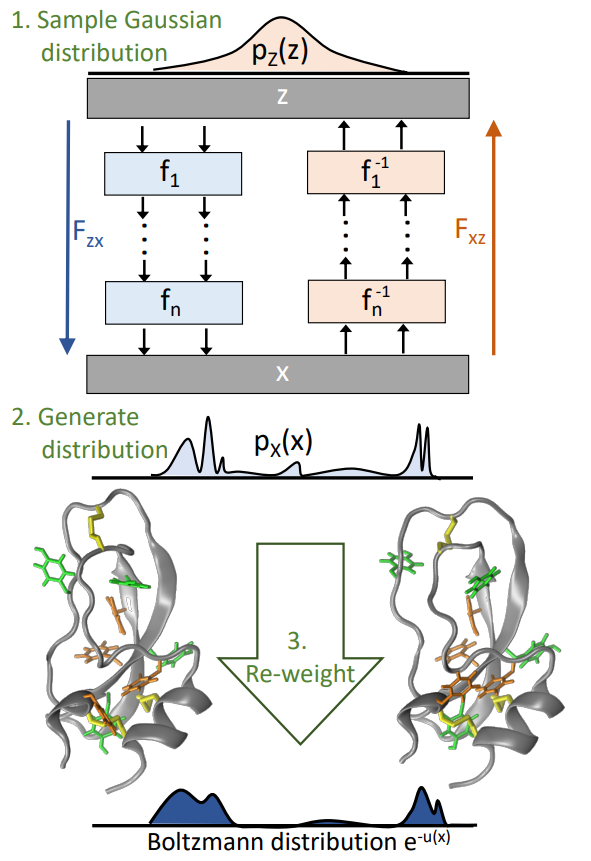Boltzmann Generator

分布的变换

无论在训练过程还是重加权过程中，对于生成构想 $\mathbf{x}$ 的概率 $p_X(\mathbf{x})$ 的计算都是关键。当神经网络 $F_{zx}$ 可逆时，这样的生成可以比较简单地进行。物理上，可逆变换类似于将概率密度从构象空间变换到潜在空间或反向的流体流动，因而，可以借助生成模型中的流模型进行处理。通常，保持体积的分布变换可以类比为不可压缩的流体，而 BG 中采用的是允许体积变化的分布变换，对应于可压缩流体的行为，因为这类模型允许在构象空间的不同部分不同地缩放概率分布。这一切的基础是可逆的神经网络结构:

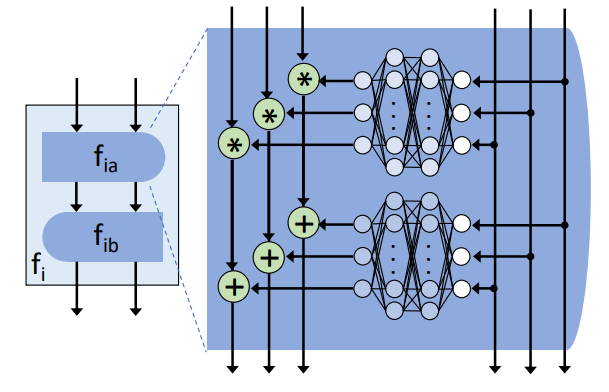Invertible Neural Block

模型的训练

主要分为两种模式: 基于能量的训练和基于例子的训练

Energy-based

采样 $\mathbf{z}$ 变换得到 $\mathbf{x}=F_{zx}(\mathbf{z})$，进而得到 $p_X(\mathbf{x})$。最小化 $p_X(\mathbf{x})$ 和原有的 Boltzmann 分布之间的差距，其中的度量可以选择 Kullback-Leibler Divergence 等。

$$J_{KL} = \mathbb{E}_{\mathbf{z}}[u(F_{zx}(\mathbf{z}))-\log R_{zx}(\mathbf{z})]$$

其中 $R_{zx}$ 是 BG 的 Jacobian 矩阵的秩。将 KL 散度作为损失函数，可以进行 BG 的训练。同时，KL 散度等价于从生成 $\mathbf{z}$ 使用的先验分布到生成的分布之间的自由能变: 表达式中的第一项代表系统的平均势能，而第二项等价于在选定温度下的熵贡献 (相差常数)。 因而，这样一个损失函数决定了模型倾向于采样低能量的结构，且可以避免模式崩塌 (mode-collapse)。

Example-based

仅仅使用基于能量的训练将使得模型有对于最稳定的亚稳态的偏好，为了处理这一问题，需要追加基于数据实例的训练。通过选取一些合法的构象 $\mathbf{x}$ (通过短 MD 等方式或使用实验数据等)，并将其映射得到 $\mathbf{z}=F_{xz}(\mathbf{x})$。此时可以进行最大似然的训练:

$$J_{ML} = \mathbb{E}_{\mathbf{x}}\left[\frac{1}{2} \left\| F_{xz}(\mathbf{x}) \right\|^2 - \log R_{xz}(\mathbf{x})\right]$$

这样基于例子的训练往往在训练早期引入，从而引导 $F_{zx}$ 关注状态空间中我们感兴趣的部分。

重要细节

可逆的可训练层: RealNVP^[2]

将变量分为两个通道 $\mathbf{x}=(\mathbf{x}_1,\mathbf{x}_2), \mathbf{z}=(\mathbf{z}_1,\mathbf{z}_2)$，在每一个通道上只进行可逆的加法和乘法操作。使用任意的，无需可逆的神经网络 $S$ 和 $T$ 分别使用第一个输入通道 $\mathbf{x}_1$ 的非线性变换对第二个输入通道 $\mathbf{x}_2$ 进行缩放和平移:

$$\begin{aligned} f_{x z}\left(\mathbf{x}_1, \mathbf{x}_2\right):&\left\{\begin{array}{l} \mathbf{z}_1=\mathbf{x}_1 \\ \mathbf{z}_2=\mathbf{x}_2 \odot \exp \left(S\left(\mathbf{x}_1 ; \boldsymbol{\theta}\right)\right)+T\left(\mathbf{x}_1 ; \boldsymbol{\theta}\right) \end{array}\right. \\ \log R_{x z}=&\sum_i S_i\left(\mathbf{x}_1 ; \boldsymbol{\theta}\right) \\ f_{zx}\left(\mathbf{z}_1, \mathbf{z}_2\right):&\left\{\begin{array}{l} \mathbf{x}_1=\mathbf{z}_1 \\ \mathbf{x}_2=(\mathbf{z}_2-T(\mathbf{x}_1;\boldsymbol{\theta}))\odot \exp (-S(\mathbf{z}_1;\boldsymbol{\theta})) \end{array}\right. \\ \log R_{z x}=&-\sum_i S_i\left(\mathbf{z}_1 ; \boldsymbol{\theta}\right) \\ \end{aligned}$$

由此可以得到 RealNVP Block

$$(\mathbf{y}_1,\mathbf{y}_2) = f_{xy}(\mathbf{x}_1,\mathbf{x}_2)\\ (\mathbf{z}_1,\mathbf{z}_2) = f_{yz}(\mathbf{y}_1,\mathbf{y}_2)$$

KL 散度的推导

隐空间中的 KL 散度

KL 散度定义如下

$$\begin{aligned} KL(q||p) &= \int q(\mathbf{x})[\log q(\mathbf{x}) - \log p(\mathbf{x})] \mathrm{d}x \\ &= -H_q - \int q(\mathbf{x})\log p(\mathbf{x}) \mathrm{d}x \\ \end{aligned}$$

其中 $H_q$ 是分布 $q$ 的熵。根据定义，若将真实的 Boltzmann 分布记为 $\mu$，生成的分布记为 $q$，那么

$$\begin{aligned} KL(\mu_Z||q_Z) &= -H_Z - \int \mu_Z(\mathbf{z}) \log q_Z(\mathbf{z};\boldsymbol{\theta}) \mathrm{d} \mathbf{z} \\ &=- H_Z - \int \mu_Z(\mathbf{z})[\log \mu_X(F_{zx}(\mathbf{z};\boldsymbol{\theta}))+\log R_{zx}(\mathbf{z};\boldsymbol{\theta})]\mathrm{d}\mathbf{z}\\ &=- H_Z + \log Z_X + \mathbb{E}_{\mathbf{z}\sim \mu_Z(\mathbf{z})}[u(F_{zx}(\mathbf{z};\boldsymbol{\theta}))-\log R_{zx}(\mathbf{z};\boldsymbol{\theta})] \end{aligned}$$

其中 $Z_X$ 满足

$$\mu_X(\mathbf{x}) = Z_x^{-1} e^{-\beta U(\mathbf{x})}$$

由于在训练过程中 $H_Z$ 和 $Z_X$ 不随 $\boldsymbol{\theta}$ 变化，可以将 KL 部分的损失函数写作

$$J_{KL} = \mathbb{E}_{\mathbf{z}\sim \mu_Z(\mathbf{z})}[u(F_{zx}(\mathbf{z};\boldsymbol{\theta}))-\log R_{zx}(\mathbf{z};\boldsymbol{\theta})]$$

若同时在多个温度下训练，那么

$$J_{KL}^{T_{1}, \ldots ,T_K} = \sum_{k=1}^K \mathbb{E}_{\mathbf{z}\sim \mu_Z^k(\mathbf{z})}[u^k(F_{zx}(\mathbf{z};\boldsymbol{\theta}))-\log R_{zx}(\mathbf{z};\boldsymbol{\theta})]$$

构象空间中的 KL 散度

类似的可以推导构象空间中的 KL 散度。

$$\begin{aligned} \mathrm{KL}_{\boldsymbol{\theta}}\left[\mu_X \| q_X\right] & =H_X-\int \mu_X(\mathbf{x}) \log q_X(\mathbf{x} ; \boldsymbol{\theta}) \mathrm{d} \mathbf{x} \\ & =H_X-\int \mu_X(\mathbf{x})\left[\log \mu_Z\left(F_{x z}(\mathbf{x} ; \boldsymbol{\theta})\right)+\log R_{x z}(\mathbf{z} ; \boldsymbol{\theta})\right] \mathrm{d} \mathbf{x} . \\ & =H_X+\log Z_Z+\mathbb{E}_{\mathbf{x} \sim \mu(\mathbf{x})}\left[\frac{1}{\sigma^2}\left\|F_{x z}(\mathbf{x} ; \boldsymbol{\theta})\right\|^2-\log R_{x z}(\mathbf{x} ; \boldsymbol{\theta})\right] \end{aligned}$$

其中 $Z_Z$ 满足

$$\mu_Z^{k}(\mathbf{z}) = Z_Z^{-1} \exp \left({-\frac{\left\| \mathbf{z} \right\|^2}{2\sigma_k^2}}\right)$$

由于从 $\mu_X$ 中进行采样是不现实的，因此这个散度项很难直接求算。但对于基于例子的训练来说，可以从给定的初始分布 $\rho(\mathbf{x})$ 开始训练，此时

$$\begin{aligned} J_{ML} &= -\mathbb{E}_{\mathbf{x}\sim \rho(\mathbf{x})}[\log q_X(\mathbf{x};\boldsymbol{\theta})] \\ &= \mathbb{E}_{\mathbf{x} \sim \rho(\mathbf{x})}\left[\frac{1}{\sigma^2}\left\|F_{x z}(\mathbf{x} ; \boldsymbol{\theta})\right\|^2-\log R_{x z}(\mathbf{x} ; \boldsymbol{\theta})\right]\\ \end{aligned}$$

KL 散度与自由能

$H_X$ 可以改写如下

$$\begin{aligned} H_X &= -\mathbf{\int_x} q_X(\mathbf{x}) \log q_X(\mathbf{x}) \mathrm{d}\mathbf{x} \\ &= - \mathbf{\int_z} q_X(F_{zx}(\mathbf{z})) \log(q_X(F_{zx}(\mathbf{z}))R_{zx}(\mathbf{z})) \mathrm{d}\mathbf{z}\\ &=-\mathbf{\int_z} \mu_Z(\mathbf{z}) \log q_X(F_{zx}(\mathbf{z})) \mathrm{d}\mathbf{z}\\ &=-\mathbf{\int_z} \mu_Z(\mathbf{z}) \log(\mu_Z(\mathbf{z})R_{zx}(\mathbf{z})^{-1}) \mathrm{d}\mathbf{z}\\ &=H_Z + \mathbb{E}_{\mathbf{z}\sim \mu_Z(\mathbf{z})}[\log R_{zx}(\mathbf{z})] \end{aligned}$$

代入 $J_{KL}$ 的表达式即有

$$J_{KL} = U - H_X + H_Z$$

此外，可以证明

$$\begin{aligned} \mathrm{KL}_{\boldsymbol{\theta}}[\mu_Z||q_Z] &= -H_Z + \log Z_X + \mathbb{E}_{\mathbf{z}\sim \mu_Z(\mathbf{z})}[u(F_{zx}(\mathbf{z};\boldsymbol{\theta})) - \log R_{zx}(\mathbf{z};\boldsymbol{\theta})] \\ &=-H_X + \log Z_X + \mathbb{E}_{\mathbf{z}\sim \mu_Z(\mathbf{z})}[u(F_{zx}(\mathbf{z};\boldsymbol{\theta}))]\\ &=- H_Z + \log Z_X + \mathbb{E}_{\mathbf{x}\sim \mu_X(\mathbf{x};\boldsymbol{\theta})}[u(\mathbf{x})]\\ &=\mathrm{KL}_{\boldsymbol{\theta}}[q_X||\mu_X] \end{aligned}$$

---

1. https://arxiv.org/pdf/1812.01729.pdf ↩︎

2. https://arxiv.org/pdf/1605.08803.pdf ↩︎